Kinetic Theory of Gases: Concepts, Applications, and Insights

The Kinetic Theory of Gases is a fundamental scientific theory that explains the macroscopic properties of gases, such as pressure, temperature, and volume, based on the microscopic behavior of gas molecules. It provides a framework for understanding how individual gas molecules move, collide, and interact with each other, leading to the observable characteristics of gases. According to this theory, gases exist as numerous tiny molecules or atomic particles which continuously move randomly throughout the system. Gas molecules create pressure when they collide with the walls of the container while their average kinetic energy is directly proportional to the temperature of the gas.

The Kinetic Theory provides insights into how gases work while describing the relationship between microscopic and macroscopic processes within thermodynamics. Gas laws including Boyle's Law, Charles’s Law, and Avogadro’s Law can be derived from kinetic theory of gases that can be used to describe the relation between pressure, volume, and temperature.

Postulates of Kinetic Theory of Gases:

The Kinetic Theory of Gases can be explained through essential fundamental postulates which explain how gas molecules act on a microscopic level. These fundamental postulates provide explanations for the macroscopic properties like pressure, temperature, and volumes of the gas. The main postulates that form the basis of the Kinetic Theory of Gases include:

1. Gases Consist of Tiny Particles

A gas contains numerous tiny elemental particles either atoms or molecules. These particles are in constant random motion in all directions, and the size of the gas (ideal gas) molecules is negligible compared to the distance between them

2. Elastic Collisions

In perfectly elastic collisions, gas molecules collide with each other and with the walls of the container without any loss of kinetic energy during these collisions.

The system maintains its entire energy value throughout the collision.

3. No Intermolecular Forces

There are no attractive or repulsive forces between gas molecules, except during collisions
 

4. Kinetic Energy and Temperature

The average kinetic energy of the gas molecules is directly proportional to the temperature of the gas, measured in Kelvin.
 

5. Continuous and Random Motion

Gas molecules are in continuous random motion, traveling in straight lines until they collide with another molecule or the container's walls. The speed of the molecules varies, with a distribution of velocities at any given time.

6. Gas Pressure and Molecular Collisions

The walls of the container experience pressure which occurs when gas molecules strike it. 

Fundamental Concepts of the Kinetic Theory of Gases

According to the Fundamental Kinetic Theory of Gases, the microscopic motion of molecules combined with their interactions between each other defines the behavior of gases. The application of fundamental concepts enables people to develop important gas laws as well as determine the physical characteristics of gases under different conditions. This theoretical concept serves as an essential basis for studying thermodynamic processes together with gas dynamics and gas behavior that occur across fields of chemistry and engineering.
 

The principles from this theory enable us to derive essential gas laws through mathematical derivations that result in Boyle's Law together with Charles’s Law and Avogadro’s Law and the Ideal Gas Law. Here’s a detailed breakdown of the important gas laws:

1. The Ideal Gas Law (PV = nRT)

The Ideal Gas Law defines relationships between pressure, volume, temperature and molecule number or mole count.

The pressure exerted by the gas is:

P=⅓ *N/V *m*v_avg²

where:

• N is the number of molecules,
• V is the volume of the gas,
• m is the mass of each molecule,
• v_avg² avg is the average velocity of the molecules.

The average kinetic energy KEavg​ of the gas molecules is:

KE_avg​= 3/2 ​k_B​T

Where k_B​ is the Boltzmann constant, and T is the temperature in Kelvin.

Since ½ mv_avg²=3/2 k_BT, we can substitute this into the pressure equation:

P= ⅔ * N/V * 3/2 k_BT

P= N/V k_BT

Finally, using the relationship N=nN_A (where n is the number of moles and N_A​ is Avogadro's number), we get:

P=nRT/V

where R=N_Ak_B​ is the universal gas constant.

This is the Ideal Gas Law:

PV=nRT

where:

• P = pressure,
• V = volume,
• n = number of moles,
• R = universal gas constant,
• T = temperature.

2. Boyle’s Law (P ∝ 1/V at constant T)

According to Boyle's Law,  for a given amount of gas at constant temperature, the pressure and volume are inversely proportional to each other. We can derive this from the Ideal Gas Law.

Keeping temperature constant (T constant) and the number of moles fixed, we can rearrange the Ideal Gas Law:

P=nRT/V

Since n and T are constants, this implies that:

P∝1/V

This is Boyle's Law, which clearly shows that as the volume of a gas decreases, its pressure increases, provided the temperature and the number of moles remains constant.

3. Charles’s Law (V ∝ T at constant P)

According to Charles’s Law, the volume of a gas is directly proportional to its temperature, keeping the pressure constant.

Start with the Ideal Gas Law, keeping the pressure constant:

P=nRT/V

Since P is constant, we can write:

V∝T

As you can see, the temperature of a gas increases, its volume increases, provided the pressure and the number of moles remains constant. This is Charles’s Law.

4. Avogadro’s Law (V ∝ n at constant P and T)

Avogadro's Law states that the volume of a gas is directly proportional to the number of moles of gas at constant pressure and temperature.

From the Ideal Gas Law:

PV=nRT

Keeping temperature and pressure constant, gives:

V∝n

Volume of a gas increases with the number of moles, provided the temperature and pressure remain unchanged.

5. Dalton’s Law of Partial Pressures

Dalton's Law states that the total pressure exerted by a mixture of non-reacting gases is the sum of the partial pressures of each individual gas within the gas mixture.

If we have a mixture of gases, the partial pressure of each gas is given by:
P_i=n_iRT/V

where P_i​ is the partial pressure of gas i, n_i​ is the number of moles of gas i, and T and V are the total temperature and volume of the mixture.

The total pressure is the sum of the partial pressures:

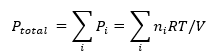
This is Dalton’s Law of Partial Pressures.

Law of Equipartition of Energy

The Law of Equipartition of Energy states that at thermal equilibrium, energy is equally distributed among all the available degrees of freedom of a system. 

Each degree of freedom contributes ½ kBT to the total energy of the system, where:

• k_B is the Boltzmann constant,
• T is the temperature in Kelvin.

Degrees of Freedom:

Translational Degrees of Freedom: Movement of particles in space (x, y, and z directions for a 3D system). Monatomic gases (including helium and neon) have 3 translational degrees of freedom.

Rotational Degrees of Freedom: Movement of molecules around axes. A linear molecule contains two rotational degrees of freedom while a nonlinear molecule has three rotational degrees of freedom.

Vibrational Degrees of Freedom: Involves both the kinetic and potential energy of a vibrating molecule. Every vibrational mode has two degrees of freedom, one for kinetic energy and one for potential energy.

What do you mean by mean-free path?

Mean free path: Mean free path refers to the average distance a gas molecule travels before colliding with another molecule.

The mean free path depends on three factors: temperature, pressure, and molecular size.

Temperature: An increase in temperature causes molecules to speed up, resulting in more numbers of molecular collisions that reduce the mean free path.

Pressure: When you increase pressure, more molecules are packed in a specific volume which shortens the mean free path.

Molecular Size: Larger molecules have a larger cross-sectional area for collisions, leading to a shorter mean-free path. Larger molecules have frequent collisions due to their greater cross-sectional areas, shortening their mean free path.